- 1.
- The function declaration line. The output arguments K1
and k2 are both whole images: that is, for
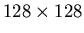 PET data, they will be column vectors with 16,384 elements.
filename is the name of the MINC file to process,
slice specifies which slice from the file to process, and
progress indicates whether or not the program should print
progress information as it goes. filename and slice
are both required; if progress is not given, it defaults to 1
(``true'').
PET data, they will be column vectors with 16,384 elements.
filename is the name of the MINC file to process,
slice specifies which slice from the file to process, and
progress indicates whether or not the program should print
progress information as it goes. filename and slice
are both required; if progress is not given, it defaults to 1
(``true'').
function [K1,k2] = rcbf1 (filename, slice, progress)
- 2.
- Get the images and image information. This includes all of the
frames for the slice being analyzed, the frame start times, the
frame lengths, the mid-frame times, and the blood data. The frame
time information is returned by simple enquiries with the data
handle img returned by openimage. The blood data is
returned by resampleblood, which gives the blood data in an
evenly sampled time domain (every half second). The blood data is
then cross-calibration corrected by multiplying by the factor
XCAL. The cross-calibration converts from
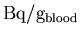 to
to
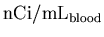 ,
taking into
account the calibration between the well counter and the PET
scanner. In order to maintain consistent units throughout the
analysis, this data must then be converted from
,
taking into
account the calibration between the well counter and the PET
scanner. In order to maintain consistent units throughout the
analysis, this data must then be converted from
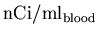 back to
back to
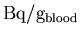 .
The actual PET
images are then retrieved, and the units are again converted to
.
The actual PET
images are then retrieved, and the units are again converted to
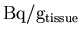 .
Any negative values present in
the images are set to zero.
.
Any negative values present in
the images are set to zero.
img = openimage(filename);
FrameTimes = getimageinfo (img, 'FrameTimes');
FrameLengths = getimageinfo (img, 'FrameLengths');
MidFTimes = FrameTimes + (FrameLengths / 2);
[g_even, ts_even] = resampleblood (img, 'even');
% Apply the cross-calibration factor, and convert back to Bq/g_blood
XCAL = 0.11;
g_even = g_even*XCAL*37/1.05;
Ca_even = g_even; % no delay/dispersion correction
PET = getimages (img, slice, 1:length(FrameTimes));
PET = PET * 37 / 1.05; % convert to decay / (g_tissue * sec)
PET = PET .* (PET > 0); % set all negative values to zero
ImLen = size (PET, 1); % num of rows = length of image
- 3.
- Calculate some useful integrals that are used several times in
the rest of the program. PET_int1, and PET_int2 are
weighted integrals of the PET data across frames (integrated with
respect to time). In particular, PET_int1 is the numerator
of the left-hand-side of equation 6, and
PET_int2 is the denominator. To get clean images out of the
analysis, we wish to set all points outside of the head to zero.
Therefore, we create a simple mask, and apply it to the weighted
integrals. Note the use of rescale to perform an
``in-place'' multiplication on PET_int1. This has the same
effect as the more conventional MATLAB
PET_int1 = PET_int1 .* mask, but without making a copy of PET_int1.
PET_int1 = trapz (MidFTimes, PET')';
PET_int2 = trapz (MidFTimes, PET' .* (MidFTimes * ones(1,ImLen)))';
mask = PET_int1 > mean (PET_int1);
rescale (PET_int1, mask);
rescale (PET_int2, mask);
- 4.
- Calculate the left hand side of equation (6).
rL = PET_int1 ./ PET_int2;
- 5.
- Assign the k2 values to be used in the lookup table, and then
generate some more useful weighted integrals. findintconvo
computes the function
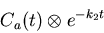 |
(15) |
at all points in the evenly-resampled time domain ts_even.
Then, it integrates across each individual frame (which run from T1to T2; T1 and T2 in the following formula are implicitly
functions of the frame). Then, the weighted integrals across all frames
are computed:
![\begin{displaymath}\int_{0}^{T} \frac
{\int_{T_1}^{T_2} \left[ C_{a}(u) \otimes e^{-k_{2}u} \right] du}
{T_2 - T_1}
w_i dt
\end{displaymath}](img30.gif) |
(16) |
Here, wi is the weighting function; for the double-weighted
analysis it is either 1 or t as in the right hand side of equation
(6).
Then, since we wish to relate k2 to the values of these integrals,
findintconvo computes equation 16 at a wide range
of values of k2 (supplied by the argument k2_lookup) for
each weighting function wi. (For the double-weighted method, w1
= 1 and w2 = t.) Note that the supplied value of
k2_lookup implies an assumption that no voxel in the image
will have a k2 value outside the range
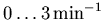 .) See section 3.3.4 for
information on the internal details of findintconvo.
.) See section 3.3.4 for
information on the internal details of findintconvo.
k2_lookup = (0:0.02:3) / 60;
[conv_int1, conv_int2] = findintconvo (Ca_even, ts_even, k2_lookup,...
MidFTimes, FrameLengths, 1, MidFTimes);
- 6.
- Calculate the right side of equation (6).
rR = conv_int1 ./ conv_int2;
- 7.
- Generate the k2 image through table lookup. This is where we
make use of the lookup tables generated in findintconvo for
great time savings: findintconvo only has to compute equation
16 (a comparatively slow operation) a few hundred
times, but for that effort we get 16,384 values of k2 very
quickly.
k2 = lookup(rR, k2_lookup, rL);
- 8.
- Generate the K1 image through table lookup and division.
k2_conv_ints contains the values of equation 16
at the actual values of k2 for this image, rather than at the
artificial set k2_lookup. This step is where we solve the
numerator of equation 6 for K1.
k2_conv_ints = lookup (k2_lookup, conv_int1, k2);
K1 = PET_int1 ./ k2_conv_ints;
- 9.
- Clean up the K1 image by setting any NaN's and infinities to
zero, and close the image data set.
nuke = find (isnan (K1) | isinf (K1));
K1 (nuke) = zeros (size (nuke));
closeimage (img);
- 10.
- Finally, K1 is converted from the internal units [
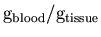 ]
to the standard units for rCBF
analysis [
]
to the standard units for rCBF
analysis [
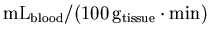 ].
].
rescale (K1, 100*60/1.05);
![]() .) See section 3.3.4 for
information on the internal details of findintconvo.
.) See section 3.3.4 for
information on the internal details of findintconvo.
![\begin{displaymath}\int_{0}^{T} \frac
{\int_{T_1}^{T_2} \left[ C_{a}(u) \otimes e^{-k_{2}u} \right] du}
{T_2 - T_1}
w_i dt
\end{displaymath}](img30.gif)